Hệ số tương quan (Correlation Coefficient) là nhiều từ được nghe đến rất nhiều đặc trưng trong nghành tài chính. Vậy ý nghĩa sâu sắc của Correlation Coefficient là gì? Làm thay nào để giám sát và đo lường được cực hiếm của thông số này?
Những vướng mắc đó sẽ được Làm Chủ Tài Chính đáp án một cách dễ nắm bắt nhất thông qua bài viết dưới đây.
Bạn đang xem: Công thức tính hệ số tương quan
Hệ số đối sánh tương quan (Correlation Coefficient) là gì?
Hệ số đối sánh là chỉ số trong thống kê học bộc lộ mối contact giữa hai biến chuyển số cùng với nhau.Hệ số tương quan chỉ nhận các giá trị trong vòng từ -1,0 đến +1,0. Nếu quý hiếm tính được nằm ngoài khoảng chừng (-1,1) thì những bị coi là tính toán không đúng hoặc đã tất cả lỗi trong thực hiện phép đo tương quan.

Nếu hệ số đối sánh có cực hiếm âm (-) và to hơn -1 thì ta nói quan hệ của hai biến chuyển là nghịch trở thành hay đây là tương quan tiền âm. Nghĩa là lúc giá trị của một biến tăng lên thì cực hiếm của biến sót lại sẽ bớt và ngược lại.
Khi hai biến đổi là nghịch biến hoàn hảo nhất thì hệ số đối sánh là bởi -1.
Ngược lại, nếu hệ số đối sánh có quý giá dương (+) và nhỏ tuổi hơn 1 thì ta nói mối quan hệ của hai vươn lên là là đồng biến đổi hay đó là tương quan liêu dương. Nghĩa là lúc giá trị của một biến tạo thêm thì cực hiếm của đổi thay còn lại cũng sẽ tăng lên.
Khi hai trở thành là đồng biến tuyệt vời và hoàn hảo nhất thì hệ số đối sánh tương quan là bởi +1.
Nếu có giá trị bằng 0 thì hai phát triển thành là chủ quyền với nhau, không có bất kỳ mối tương tác nào với nhau.
Có thể chỉ ra một trong những loại đối sánh bao gồm: đối sánh tương quan nội kính (ICC – Intraclass correlation), Kendall tau, Gamma Goodman, Kruskal Hệ số đối sánh đa sắc,…
Công thức tính hệ số tương quan Pearson
Có nhiều loại thông số tương quan, tuy vậy loại phổ cập nhất là đối sánh tương quan Pearson. Bên dưới đây cửa hàng chúng tôi gửi đến các bạn đọc một vài công thức tính hệ số đối sánh Pearson.
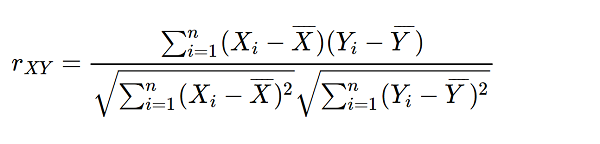
Trong đó:
rxy là hệ số đối sánh tương quan cần tìm trình diễn mối liên hệ giữa hai biến X, YXi và Yi thứu tự là những giá trị của biến đổi X và biến hóa Yn là số cực hiếm của đổi mới X và YX cùng Y theo lần lượt là các giá trị trung bình của hai biến X, YĐể tiện lợi trong tính toán, ta hoàn toàn có thể thực hiện tại theo quá trình sau:
Bước 1: xác định mẫu dữ liệu cần tính toán và đặt biến hóa X, Y tương xứng với các giá trị mẫu mã dữ liệu.Bước 2: từ mẫu tài liệu trên ta tiến hành tính cực hiếm trung bình X và YBước 3: Tính lần lượt giá trị những hiệu ai=(Xi – X ) và bi =(Yi – Y) với i là chỉ số chạy từ là một đến n.Bước 4: thứu tự nhân ai cùng với bi tương ứng, tiếp nối tính tổng các tích vừa kiếm tìm được, để là tử số.Bước 5: Tính bình phương của ai sau đó tính tổng S những giá trị bình phương của ai vừa tính được. Triển khai tính tổng S’ tương tự với bi.Bước 6: đem căn bậc hai của tích SS’, đặt là mẫu số.Bước 7: Tính quý hiếm rxybằng bí quyết lấy tử số tính được ở cách 4 phân chia cho mẫu mã số tính được ở bước 6.Ngoài ra ta rất có thể tính toán theo cách làm sau:
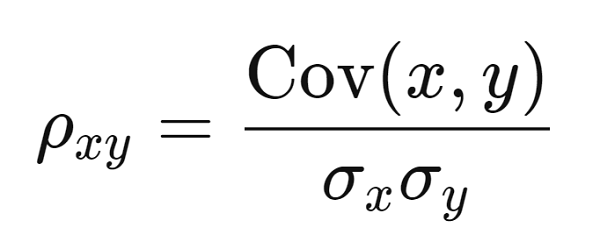
Trong đó:
ρxy: là hệ số đối sánh cần tìm trình diễn mối tương tác giữa hai biến đổi x, yCov(x, y): là hiệp phương sai của biến đổi x và biến chuyển yσx: là độ lệch chuẩn đối với đổi mới xσy: là độ lệch chuẩn đối với biến chuyển y
Độ lệch chuẩn cho ta biết độ phân tán dữ liệu so với khoảng trung bình.
Hiệp phương sai cho ta biết quan hệ tuyến tính thân hai thay đổi số.
Ví Dụ Cách Tính Hệ Số đối sánh tương quan Bằng Hàm CORREL vào Excel
Việc tính toán bằng tay thủ công ở trên sẽ mất nhiều thời gian cùng dễ tính nhầm nếu như bạn giám sát và đo lường không cẩn thận. Vì thế ta sẽ thực hiện công cụ cung ứng là hàm Correl trong trang tính Excel.
Việc sử dụng hàm Correl để giúp việc thống kê giám sát đơn giản, gấp rút và tất cả tính đúng mực cao.
Đây là cách thức rất có lợi và tương xứng với việc đo lường và thống kê lượng tài liệu lớn.
Cú pháp hàm
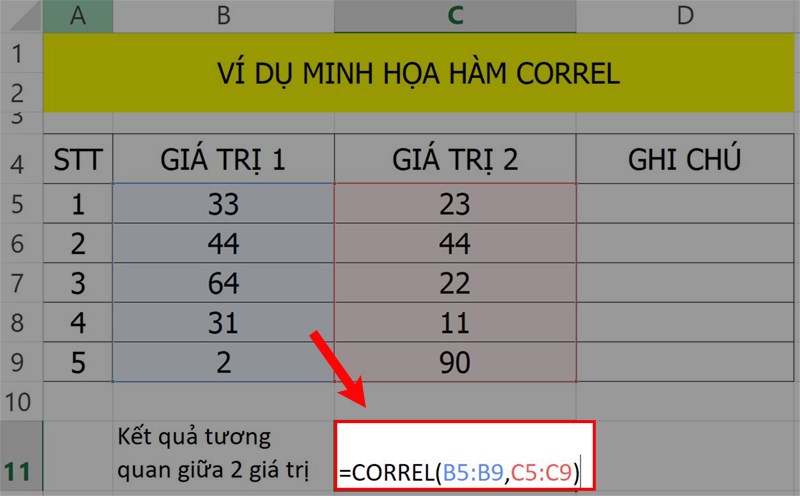
Cú pháp hàm: =CORREL(array1, array2)
Trong đó:
Array1: Là phạm vi ô chứa những giá trị của tập tài liệu thứ 1.Array2: Là phạm vi ô chứa những giá trị của tập dữ liệu thứ 2.Cách sử dụng
Ví dụ: Hãy sử dụng hàm CORREL nhằm tính thông số tương quan của các số trong bảng sau.
Bước 1: Ở bảng dữ liệu ví dụ trên bạn nhập hàm như hình vào ô tham chiếu.
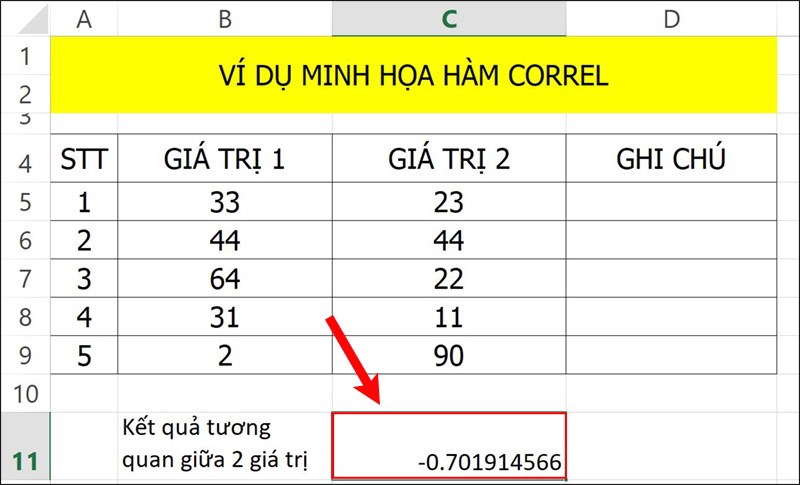
Bước 2: Bạn nhấn phím Enter để hiển thị kết quả.
Ý nghĩa của hệ số tương quan
Dựa vào hệ số đối sánh ta sẽ hiểu rằng mối contact giữa hai biến. Trải qua đó đỡ đần ta biết độ to gan lớn mật yếu trong tình dục của hai đổi thay đang xét.
Giá trị tuyệt đối của hệ số tương quan càng gần cho 1 cho ta thấy mối quan hệ giữa hai trở nên càng mạnh dạn mẽ.

Ví dụ: giá trị của hệ số tương quan bằng 0,2 mang lại ta biết mối quan hệ giữa hai biến đổi là đồng biến. Mặc dù mức độ trong quan hệ nam nữ của hai biến ở mức thấp, không đáng kể.
Các chuyên viên đã đánh giá và nhận định rằng đối sánh tương quan giữa hai biến đổi có ý nghĩa khi đạt quý giá từ 0,8 trở lên với nếu quý giá từ 0,9 trở lên thì mối contact đó khôn xiết chặt chẽ.
Do vậy, nếu quý giá dưới 0,8 thì hoàn toàn có thể bỏ qua mối đối sánh tương quan giữa hai biến đó.Với mỗi loại thông số tương quan khác nhau sẽ có một số đặc tính riêng lẻ và tất cả phạm vi áp dụng là không giống nhau.
Hệ số này như một vẻ ngoài giúp ta có thể phân tích vấn đề một cách bao gồm xác, tìm ra được xu hướng, mối quan hệ giữa các biến số để từ đó bao hàm kế hoạch vào đầu tư.
Hệ số đối sánh tương quan được hồi quy trong những phần mềm: Stata, Spss, Eview, R,…
Điều kiện nhằm hệ số tương quan Pearson sống thọ ý nghĩa
Hệ số đối sánh tương quan Pearson (ký hiệu là r) là thịnh hành nhất bây chừ trong rất nhiều loại thông số tương quan. Chỉ số r để đo những mối contact giữa nhị biến.
Đồ thị biểu diễn tương quan Pearson là 1 trong đường thẳng nhằm thể hiện quan hệ giữa hai phát triển thành mà ta vẫn xét.
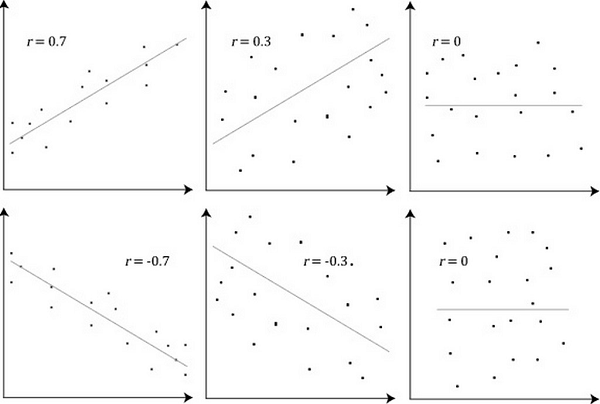
Hệ số Pearson với những điểm lưu ý chung cùng có chân thành và ý nghĩa tương từ như những hệ số đối sánh tương quan khác. Thông số r có giá trị nằm trong khoảng (-1, +1)
Nếu -1 nếu r=0 thì ta thấy thân hai biến không có sự đối sánh tương quan nào.Nếu 0Trên thực tế, hệ số đối sánh Pearson chỉ giúp đỡ bạn dự đoán được gồm tồn tại mối quan hệ giữa hai thay đổi cố hay là không và nếu có thì mối quan hệ đó là tương quan âm tuyệt dương.
Để đối sánh Pearson tồn tại ý nghĩa thì cực hiếm sig. 5% thì ta tóm lại giữa nhì biến không tồn tại tương quan.
Xem thêm: 29 hình ảnh chào buổi sáng ngộ nghĩnh dễ thương nhất
Thống kê đối sánh và đầu tư chi tiêu mang lại ý nghĩa sâu sắc gì?
Hệ số tương quan là quý giá thống kê được dùng trong tương đối nhiều lĩnh vực, đặc trưng là chi tiêu tài chính.
Ngoài ra, trong việc nhận xét hiệu suất hay giao dịch định lượng thì hệ số tương quan có vai trò cực kì quan trọng.
Nhà đầu tư cần theo dõi hệ số đối sánh tương quan của gia tài riêng lẻ trong các mục mà người ta đang đầu tư. Tuy vậy vẫn cần bảo đảm tổng mức dịch chuyển được giữ tại mức giới hạn mang đến phép.

Bên cạnh đó, nhờ việc ứng dụng thông số tương quan, những nhà phân tích rất có thể dễ dàng hiểu rằng xu hướng biến đổi của khối gia tài nếu có yếu tố làm sao đó phía bên ngoài tác động đến.
Đặc biệt trong đầu tư chi tiêu tài chính, bạn sẽ càng nhận thấy sự hữu dụng của việc thống kê tương quan. Dựa vào tính hóa học của mối quan hệ nghịch biến, những nhà đầu tư chi tiêu có thể thành lập kế hoạch để bảo đảm tài sản của chính bản thân mình tránh gặp rủi ro.
Khi có sự biến đổi về giá bán thì nấc độ khủng hoảng sẽ giảm đi.
Không đầy đủ vậy, thông số tương quan còn giúp nhà chi tiêu qua đó rất có thể đánh giá bán được đâu là cơ hội mối đối sánh có thể biến hóa rõ thân 2 biến.
Ứng dụng của hệ số tương quan trong tài chính như thế nào?
Trên thực tiễn hệ số đối sánh được ứng dụng trong hầu như các nghành nghề dịch vụ và quan trọng trong nghành tài chính.
Dựa trên quý hiếm hệ số đối sánh ta sẽ có thể thấy sức mạnh của quan hệ giữa hai thay đổi số.

Để nắm rõ ứng dụng của hệ số tương quan trong tài chính, ta đi xét các trường hợp rõ ràng dưới đây:
Ví dụ: Hệ số tương quan giúp những nhà phân tích xác minh mối đối sánh giữa giá dầu thô với giá cổ phiếu của khách hàng sản xuất dầu. Có thể thấy đa số các doanh nghiệp dầu mỏ đang kiếm lợi nhuận dựa vào giá dầu tăng, có tác dụng giá cổ phiếu của bạn tăng lên. Đây là mối quan hệ đối sánh dương.
Các chỉ số tài chính được nhìn nhận như xác suất đòn bẩy và tạo thành lợi nhuận nếu như chúng tất cả mối tương quan cùng chiều với nhau. Những doanh nghiệp rất có thể tận dụng điều này để vạc triển kinh doanh vì lúc doanh nghiệp sử dụng nhiều đòn bẩy mà mang về nhiều roi tăng thì họ cần cân nhắc có cần vay vốn ngân hàng thêm để đầu tư kinh doanh xuất xắc không.
Hệ số tương quan dùng để xác định mức độ kết quả của quỹ tương hỗ so cùng với chỉ số chuẩn, hoặc những tài sản.
Như vẫn phân tích nghỉ ngơi trên, những nhà đầu tư có thể sử dụng gia sản hay kinh doanh thị trường chứng khoán có mối đối sánh tương quan nghịch vươn lên là để phòng ngừa và sút thiểu rủi ro do biến động thị trường.
Bên cạnh đó, được cho phép các nhà đầu tư có thể xác minh được khi nào mối tương tác giữa hai biến hóa sẽ nỗ lực đổi.
Ví dụ, cổ phiếu ngân hàng thường bao gồm mối contact tích rất với lãi vay do lãi suất vay hay tính dựa vào lãi suất của thị trường
Nếu giá cp của một ngân hàng đang giảm trong khi lãi suất vẫn tăng, các nhà đầu tư chi tiêu có thể đề ra nghi vấn về ngân hàng mình đầu tư chi tiêu có đang chuyển động không công dụng không.
Ngoài ra, nếu giá cổ phiếu của các ngân hàng tương tự như đều tăng thì nhà chi tiêu có thể tóm lại cổ phiếu giảm không phải do lãi suất mà do bank đó chuyển động kém hoặc nội bộ bao gồm vấn đề…
Kết luận
Mong rằng cùng với những tin tức Lamchutaichinh.vn cung cấp, bạn đọc đã gọi hơn về thông số tương quan, biết cách đo lường và rất có thể ứng dụng vào tạo ra kế hoạch trong đầu tư tài chính.
Phân tích tương quan Pearson r (cung cấp cho một hệ số tương quan Pearson, được ký kết hiệu là r) là thước đo độ mạnh mẽ của mối liên kết tuyến tính thân hai biến. Về cơ bản, sự tương quan Pearson nỗ lực vẽ một đường tương xứng nhất thông qua dữ liệu của hai biến chuyển và hệ số tương quan Pearson, r, cho biết khoảng cách toàn bộ các điểm dữ liệu này đến đường cân xứng nhất này (tức là những điểm dữ liệu này tốt như nỗ lực nào với mô hình / đường mới tương xứng nhất).
1. Bao giờ sử dụng?
Phân tích đối sánh tương quan Pearson, r, rất có thể được sử dụng làm ước lượng mẫu mã cho tương quan dân số, ρ (rho). Nó là một chỉ số không có thứ nguyên về quan hệ tuyến tính thân hai vươn lên là ngẫu nhiên, giá bán trị bằng 0 có nghĩa là không có mối quan hệ tuyến tính giữa các biến cùng giá trị bởi 1 cho biết mối quan liêu hệ tuyến đường tính trả hảo. Giả dụ mối tương quan là âm, tức là giá trị tăng bên trên một thay đổi được kết phù hợp với giá trị giảng trên vươn lên là kia. Quý hiếm của r tất cả thể biến hóa giữa −1 cùng +1 bất kỳ kích thước đo lường và tính toán của hai biến.
Tương quan tiền Pearson, r, yêu cầu được xem như là một thống kê diễn tả (descriptive statistic) lúc 1 nhà nghiên cứu và phân tích muốn định lượng mức độ của mối quan hệ tuyến tính giữa các biến. Một tương quan tham số sẽ phù hợp bất cứ khi nào các phép đo định lượng được tiến hành đồng thời trên hai hoặc những biến, mối quan hệ giữa hai biến hóa là đường tính với cả hai trở thành đều được trưng bày chuẩn. Các mối tương quan phải luôn luôn được khám nghiệm trước khi triển khai các phân tích nhiều biến tinh vi hơn, ví dụ như phân tích nhân tố (factor analysis) hoặc so với thành phần bao gồm (principal component analysis). Cường độ của mối quan hệ tuyến tính giữa hai biến số có thể khó review từ biểu đồ phân tán và thông số tương quan cung ứng một phiên bản tóm tắt ngăn nắp hơn. Tuy nhiên, sẽ không khôn ngoan nếu nỗ lực tính toán mối tương quan khi biểu thứ phân tán thể hiện một mối quan hệ phi tuyến tính rõ ràng. Lúc một nhà nghiên cứu xem xét cả mức khoảng rộng và chân thành và ý nghĩa của một mối đối sánh tương quan thì r được sử dụng theo phong cách suy diễn như một mong lượng của mối đối sánh dân số, ρ (rho).
Công thức tính hệ số đối sánh tương quan Pearson vào hai trở nên x với y từ n mẫu mã như sau:
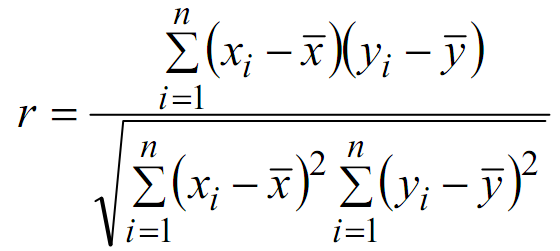
2. Mang thuyết vô hiệu và suy luận thống kê
Khi mong lượng kích thước của mối đối sánh tương quan dân số, bạn cũng có thể muốn chất vấn xem nó có chân thành và ý nghĩa thống kê tuyệt không. Mang thuyết vô hiệu là H0: ρ = 0, nghĩa là, đổi thay X không tương quan tuyến tính với biến hóa Y. Mang thuyết sửa chữa thay thế là H1: ρ ≠ 0. đưa thuyết vô hiệu là 1 trong những phép bình chọn xem có bất kỳ mối quan lại hệ ví dụ nào giữa các biến X và Y rất có thể phát sinh một cách vô tình hay không. Bày bán mẫu của r là không chuẩn khi tương quan dân số lệch khỏi 0 và khi kích cỡ mẫu bé dại (n Fisher’s z.
3. Các giả định thống kê
Trong một trong những sách thống kê giành riêng cho các nhà kỹ thuật xã hội, bạn ta xác minh rằng để thực hiện mối đối sánh tương quan Pearson, cả hai đổi mới phải có phân phối chuẩn, nhưng trong những văn bạn dạng khác, nó bảo rằng phân phối của tất cả hai biến bắt buộc đối xứng (symmetrical) và đơn phương (unimodal) nhưng mà không tuyệt nhất thiết đề xuất chuẩn. Những chủ kiến này gây hoang mang lo lắng lớn cho những nhà phân tích và cần được thiết kế rõ. Nếu như thống kê tương quan chỉ được thực hiện cho mục đích mô tả thì không quan trọng phải sử dụng những giả định chuẩn về hiệ tượng (form) của trưng bày dữ liệu. Những giả định nhất được yêu mong là:
các phép đo định lượng (mức khoảng hoặc mức tỷ lệ của phép đo) được thực hiện đồng thời trên nhì hoặc nhiều biến hóa ngẫu nhiên. Có nghĩa là hai biến phải được thống kê giám sát trên thang đo khoảng tầm hoặc tỷ lệ. Tuy nhiên, cả nhì biến không nhất thiết phải được thống kê giám sát trên và một thang đo (ví dụ, một biến hoàn toàn có thể là phần trăm và một hoàn toàn có thể là khoảng).các phép đo bắt cặp cho từng đối tượng (ví dụ, mọi người tham gia) là độc lập. Ví dụ, chúng ta đã thu thập thời gian ôn tập (tính bởi giờ) và tác dụng thi (đo từ bỏ 0 cho 100) từ bỏ 100 sv được lấy mẫu bỗng dưng tại một trường đại học (tức là bạn có hai vươn lên là liên tục: “thời gian ôn tập” với “kỳ thi hiệu suất”). Mỗi cá nhân trong số 100 sinh viên sẽ có một cực hiếm về thời gian ôn tập (ví dụ: “sinh viên số 1” sẽ học trong “23 giờ”) và tác dụng bài khám nghiệm (ví dụ: “sinh viên số 1” đạt “81/100”). Vị đó, bạn sẽ có 100 giá trị được ghép nối.Các công dụng thu được sẽ diễn tả mức độ mà mối quan hệ tuyến tính được áp dụng cho tài liệu mẫu.
Ngoài ra, bắt buộc nhận xét an ninh về việc thực hiện r. Đây chưa phải là phần nhiều giả định nghiêm khắc nhưng trong số những tình huống nghiên cứu và phân tích điển hình lúc r hoặc là bắt buộc được phân tích và lý giải một biện pháp thận trọng, hoặc không nên sử dụng.
Khi phương sai của hai thước đo cực kỳ khác nhau, thường tương quan đến các phạm vi khác nhau hoặc rất có thể là một phạm vi số lượng giới hạn cho một biến, thì mối tương quan mẫu đang bị hình ảnh hưởng. Ví dụ: giả dụ một đổi thay bị giảm bớt phạm vi, (một phần của phạm vi điểm số không được sử dụng hoặc ko phù hợp) thì điều này sẽ có xu phía làm giảm (thấp hơn) mối đối sánh giữa nhì biến.Khi có những giá trị nước ngoài lệ, r đề xuất được lý giải một phương pháp thận trọng.Khi các quan liền kề được đem từ một đội không đồng bộ (heterogeneous). Nếu giỏi nhất, tài liệu nên là đồng độc nhất (homoscedasticity). Đồng tuyệt nhất trong tương quan tức là các phương không đúng dọc theo đường của sự phù hợp nhất vẫn giống như khi dịch chuyển dọc theo đường. Nếu các phương sai không giống nhau thì bao gồm phương sai biến đổi (hay nói một cách khác heteroscedasticity). Đồng tuyệt nhất (hay độ giãn nở đồng nhất) được thể hiện dễ dãi nhất bởi sơ đồ, như hình bên dưới đây: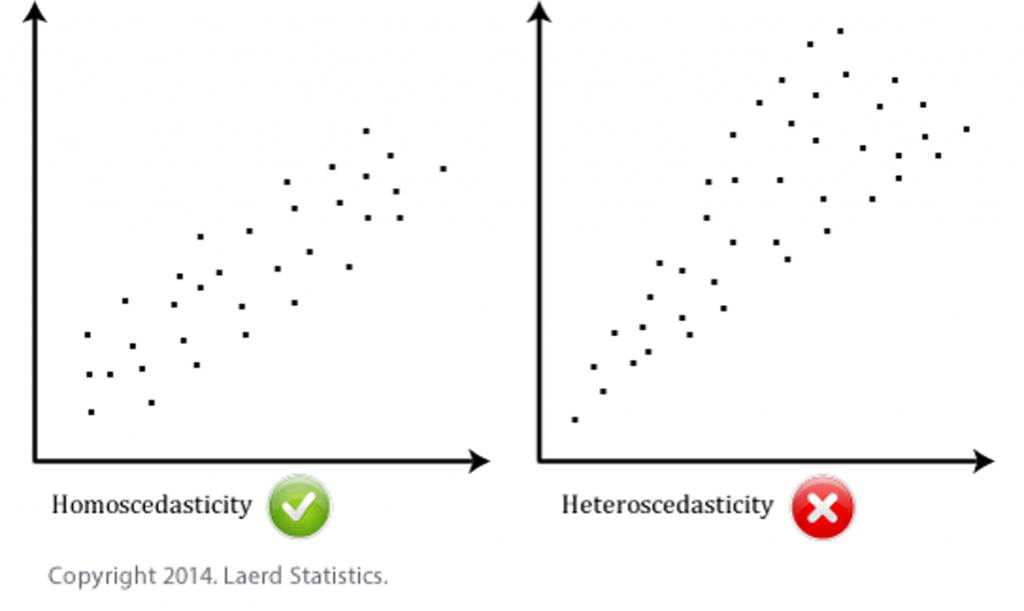
4. Phân tích tương quan Pearson r trong SPSS
Ví dụ, một nhà phân tích muốn biết liệu tác dụng kỳ thi viết cuối kì môn Toán giải thích có đối sánh với thời gian ôn tập cuối kì của các sinh viên tốt không. Có trăng tròn sinh viên được mời tham gia một cuộc demo nghiệm, kể từ khi bài học của môn Toán giải tích kết kết mang đến ngày thi cuối kì, chúng ta được đề nghị đánh dấu tổng số giờ ôn bài bác (cộng dồn của mỗi ngày) giành cho môn Toán. Dứt kì thi, nhà phân tích thu thập điểm số của đôi mươi sinh viên này theo thang điểm 100, và tổng phù hợp theo bảng bên dưới đây.
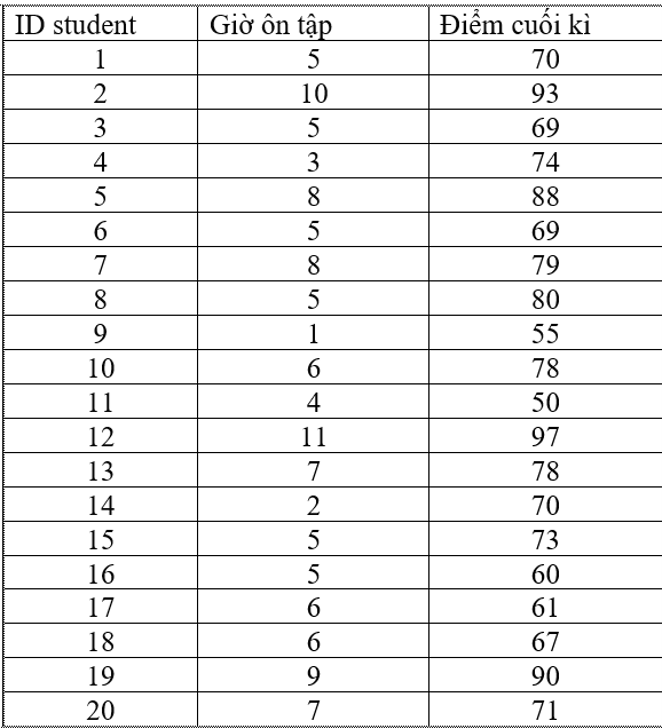
Hai câu hỏi nghiên cứu được xem như xét: i) Điểm thi viết cuối kì môn Toán giải thích có liên quan tuyến tính với khoảng thời gian ôn tập của những sinh viên xuất xắc không? cùng ii) số giờ ôn tập của những sinh viên có liên quan tuyến tính với điểm thi viết cuối kì môn Toán giải thích hay không?
Các bước tiếp sau đây hướng dẫn chúng ta cách phân tích tương quan Pearson r trong thống kê lại SPSS.
– bước 1: kiểm soát biểu vật phân tán tế bào tả quan hệ giữa nhì biến. Xin vui mắt đọc bài cách vẽ biểu đồ phân tán. Công dụng vẽ biểu đồ dùng phân tán được trình bày trong hình dưới đây.
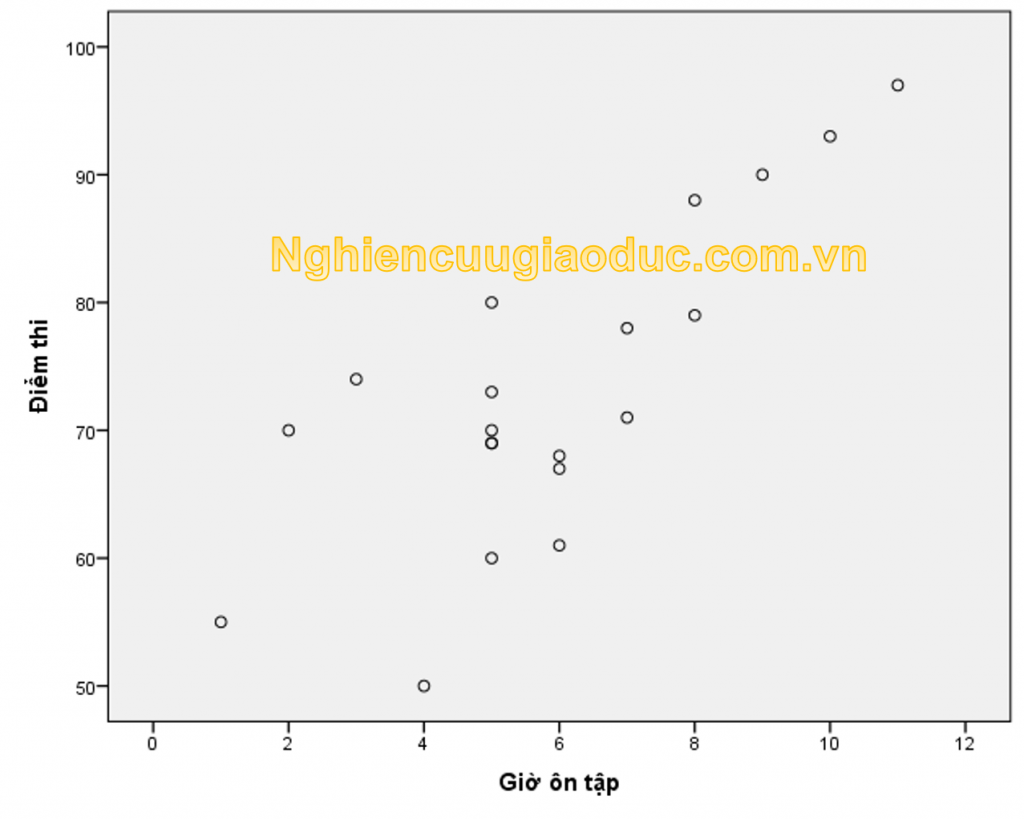
Nhận xét: Biểu vật scatter giữa Điểm thi cùng Ôn tập nhắc nhở xu hướng sát đúng tuyến đường tính, nhưng cỡ mẫu là nhỏ tuổi để quan sát cụ thể một đường tuyến tính. Vào thực tế, chúng ta cần một khuôn khổ mẫu phệ hơn, tối thiểu n > 30. Biểu trang bị này cũng cho biết một quan liền kề ngoại lệ rất cụ thể (điểm gần quý giá 4 sinh sống trục hoành).
– bước 2: lúc biểu đồ gia dụng phân tán dự đoán mối quan lại hệ con đường tính, bọn họ tiến hành phân tích tương quan Pearson r. Click Analyze-> Correlate -> Bivariate…
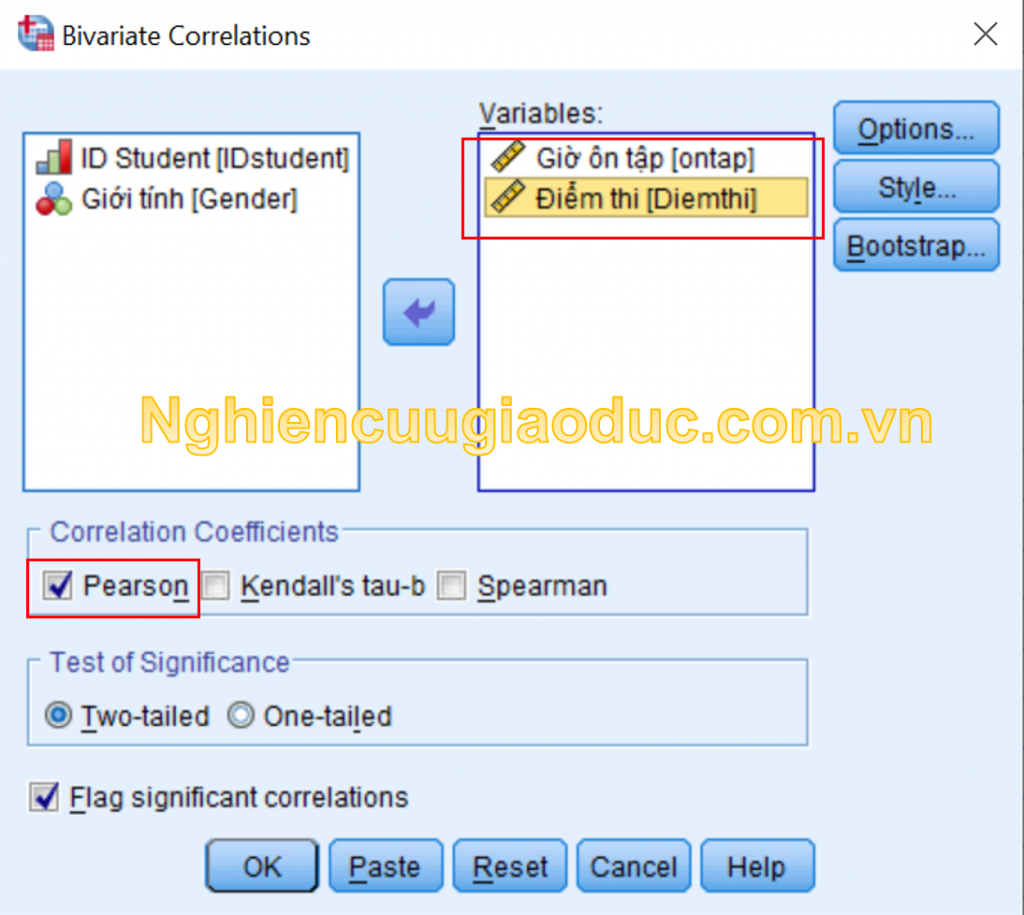
– bước 3: Trong vỏ hộp thoại Bivariate Correlations, chúng ta chuyển những biến bắt buộc kiểm tra đối sánh với nhau vào hộp Variables. để ý check vào hộp Pearson trong vùng Correlation Coefficients. Tiếp đến nhấp OK nhằm chạy kết quả.
Phân tích kết quả:
Bảng Correlations trình bày hệ số đối sánh tương quan Pearson r, giá chỉ trị chân thành và ý nghĩa p của chính nó và kích cỡ mẫu được xem toán. Trong ví dụ này, chúng ta có thể thấy rằng hệ số đối sánh Pearson, r, là 0.78 cùng nó có ý nghĩa sâu sắc thống kê (p = 0.000).
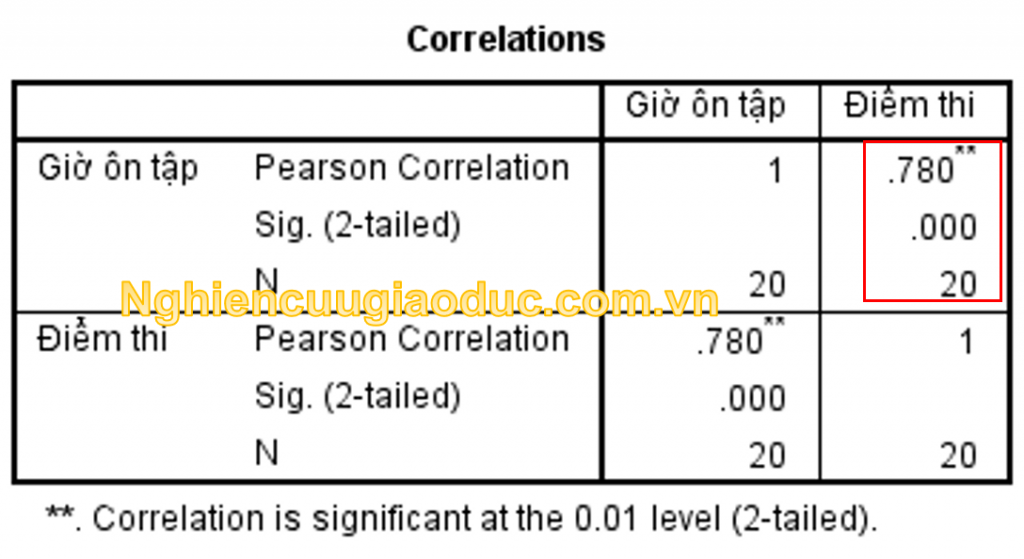
Chúng ta rất có thể viết report rằng, một đối sánh tương quan Pearson đã làm được chạy để khẳng định mối quan lại hệ tuyến tính thân Điểm thi viết cuối kì môn Toán lý giải và khoảng thời gian ôn tập của những sinh viên. Kết quả cho biết thêm có mối đối sánh thuận giữa Điểm thi viết cuối kì môn Toán lý giải và khoảng thời gian ôn tập của các sinh viên (r = 0.780, n = 20, p = 0.000).
– bước 4: Kiểm tra ý nghĩa sâu sắc của hệ số đối sánh tương quan r
Một khi mối đối sánh tương quan đã được xem toán, nhà nghiên cứu hoàn toàn có thể muốn biết tài năng xảy ra mối đối sánh tương quan thu được này như vậy nào, nghĩa là, đây bao gồm phải là sự việc xuất hiện vô tình hay nó thay mặt đại diện cho mối tương quan dân số đáng kể?
Để tiến hành việc này, r được chuyển đổi, và xác suất của quy định ước lượng này dựa trên phân phối mẫu mã của những thống kê t (t-statistic). bởi vì đó, ý nghĩa sâu sắc của một hệ số đối sánh tương quan Pearson nhận được được tấn công giá bằng cách sử dụng phân phối t (t-distribution) cùng với n − 2 bậc thoải mái (df) với được cho bởi phương trình sau:
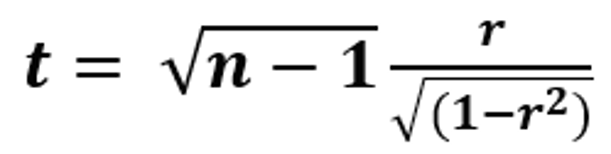
Giả thuyết loại bỏ được chu chỉnh là hai biến hóa độc lập, tức là không có quan hệ tuyến tính giữa chúng, H0: ρ = 0. Mang thuyết thay thế là, H1: ρ ≠ 0.
Để trả lời câu hỏi, bao gồm mối đối sánh tương quan đáng kể nào, ở tầm mức 5%, thân điểm Điểm thi viết cuối kì môn Toán lý giải và số giờ ôn tập của những sinh viên không? t sẽ tiến hành tính như sau:
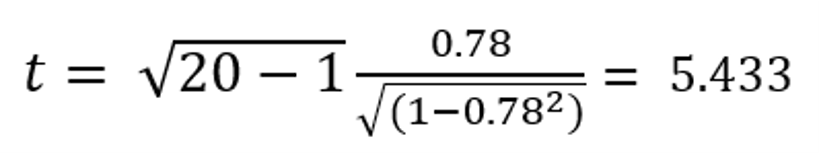
Tra bảng tới hạn của quý hiếm t (critical t-value) thu được giá trị là 2.101. Thống kê bình chọn t là quá quá quý hiếm tới hạn này, (5.433 > 2.101), và cho nên vì thế giả thuyết loại bỏ bị bác bỏ bỏ. Bọn họ kết luận rằng mối tương quan có ý nghĩa sâu sắc ở nấc 5%.
– cách 5: đánh giá khoảng tin yêu của hệ số đối sánh tương quan r
Khoảng tin yêu là dựa vào một sự chuyển đổi thống kê r thành những thống kê Fisher’s z. Điều này không hệt như độ lệch Z (Z-deviate) so với phân phối chuẩn (đôi lúc được gọi là vấn đề Z). Để diễn giải khoảng chừng tin cậy, điểm số Fisher’s z yêu cầu được đổi khác trở lại số liệu tương quan. Fisher’s z được review là:
Khoảng tin yêu (95%) mang lại mối đối sánh tương quan lưỡng biến giữa Điểm thi viết cuối kì môn Toán phân tích và lý giải và thời gian ôn tập của những sinh viên được xem bằng công thức:
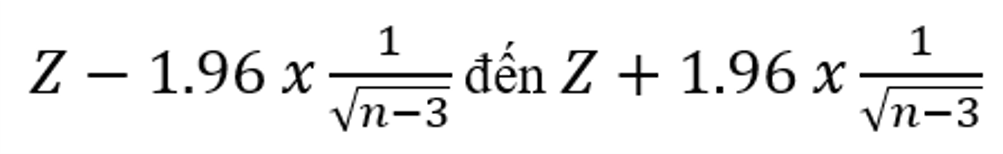
Công thức biến đổi Fisher’s Z được tư tưởng là:
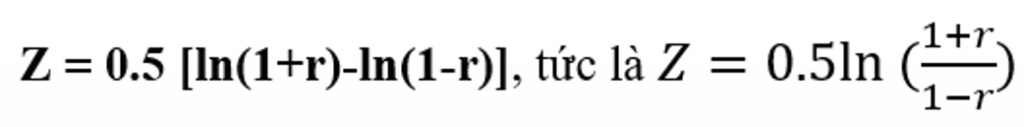
Áp dụng các công thức trong lấy một ví dụ (với r = 0.78), ta có:
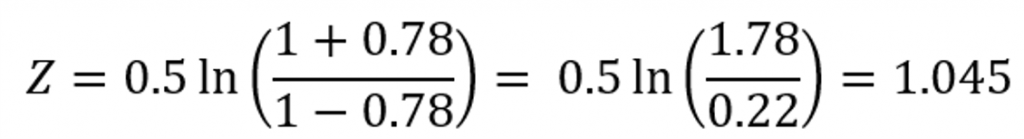
Khoảng tin cậy (95%):
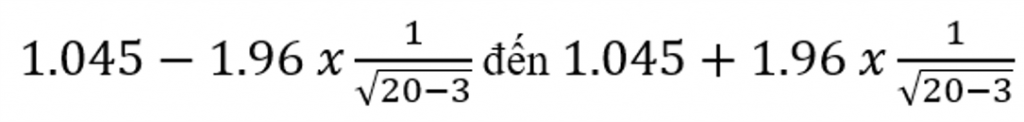
= 0.57 đến 1.52
Các cực hiếm này bây giờ phải được biến hóa trở lại số liệu ban đầu.
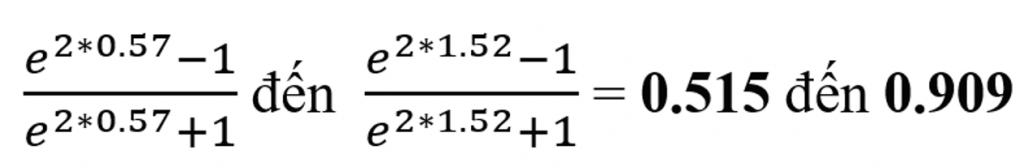
Nhận xét: chúng ta có thể kết luận rằng chúng ta chắc chắn 95% rằng mối tương quan dân số là dương và nằm trong vòng 0.515 đến 0.909. Khoảng tin cậy này không bao gồm giá trị 0, điều này cho biết thêm mối đối sánh tương quan có ý nghĩa thống kê ở tại mức 5%.














